情報処理試験で出てくる浮動小数点数って何？
floatとかdoubleとかよく分からない！
そんな悩みにお答えします。
今回は「浮動小数点数」について、実践も交えながらわかりやすく解説します。
- 浮動小数点数の仕組み
- 固定少数点数との違い
- 実際に変換してみる
注意）bit(ビット)や2進数での数の表し方は知っている前提で話を進めます。
浮動小数点数とは
浮動小数点数とは、浮動小数点方式によって、表現された数のことです。（Wikipediaより）
浮動小数点数（ふどうしょうすうてんすう、英: floating point number）は、浮動小数点方式と呼ばれる方式によって表現された数のことである。浮動小数点方式においては、固定長の仮数部と固定長の指数部の2つの部分の組み合わせによって、数値を表現す。コンピュータの数値表現において、浮動小数点方式が多用される。
https://ja.wikipedia.org/wiki/%E6%B5%AE%E5%8B%95%E5%B0%8F%E6%95%B0%E7%82%B9%E6%95%B0
じゃあその「浮動小数点方式」って何？
浮動小数点方式は、数の表し方のことです。
なぜ使う必要があるのか
浮動小数点数とは反対に、固定少数点数があります。
固定少数点数
固定少数点数はその名の通り小数点を固定して表すものです。
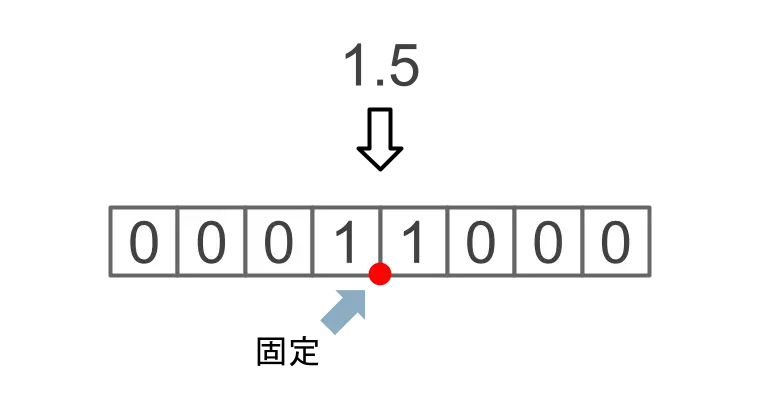
10進数の少数1.5を2進数の固定少数点数に変換しています。
このように固定少数点数では、小数点を置く位置をあらかじめ決めておき、整数部と少数部に分ます。
また、小数点を置く位置は必ずしも真ん中というわけではありません。
桁数が足りなくなる
固定少数点数は小数点が固定されているので非常にわかりやすいです。
しかし、次のような数を表そうとすると、桁が足りなくなってしまいます。
小数点を前に固定しても、小さな値だと表現しきれないことがあります。
もっと極端にいうと、「0.0000000000000001」のような数だと、はみ出てしまうことは想像がつきます。
「0 × 15」みたいな感じで0の数をまとめちゃえばいいんじゃない？
そうやって表した数が、今回紹介する浮動小数点数です。
浮動小数点数の仕組み
こちらの方式では、仮数と指数という二つの数を使って数を表現します。
正確には符号もありますが、今回は省略します。
例えば、10進数「0.000000012」を仮数と指数を使ってあらわすと次のようになります。
小数点を移動し、移動した分を指数としています。
このときの「10」は基数といい、n進数のnの部分が基数となります。（10進数なら10）
次に2進数「0.0001101」を仮数と指数で表します。
2進数なので、基数は「2」です。
小数点をうまく移動させて、指数表記に直すことを正規化といいます。
そしてこの仮数と指数を合わせて、浮動小数点数を表現します。
仮数部と指数部のビット数の割合を3と4、としたとき、2進数「0.0001101」は浮動小数点数として「10111010」と表すことができます。
先ほどは省略しましたが、正負の符号はプラスなら0、マイナスなら1を先頭のビットに追加します。
まとめ
- 浮動小数点数はとても小さい数も表現できる
- 符号、仮数、指数を使って表現する=>正規化
- 仮数に基数(2)の指数乗をかけて符号をつけると、元の形に戻せる
やってみよう
問題
10進数0.125を正規化した16ビットの浮動小数点方式で表しなさい。
左から数えて符号は1ビット、指数部は4ビット、仮数部は11ビットとし、負数は2の補数で表現する。
正の数なので符号ビットは0、指数は-2なので補数表現で1110、仮数は1なので1です。
基本情報技術者試験の勉強に使った本
私は中学3年生の時に基本情報技術者試験に合格しました。
新しい版となっていますが、こちらの本を使って勉強しました。
とてもわかりやすいのでおすすめです。
いかがだったでしょうか。
質問等あればコメントまでよろしくお願いします。
コメント
この春から未経験でエンジニアとして就職したのですが、基本情報の試験勉強をしていても？？？がいっぱいだったところ、このサイトにたどり着きました。
色使いもちょうどよく、わかりやすい説明ですぐに理解することができました。
ありがとうございます。